All I needed for FP I learned in High School Algebra
Are you tired of forgetting which keys go in which maps? Are your data transformation pipelines reaching trans-continental proportions? A smidgen of high school algebra may go a long way to eliminating your deeply nested headaches. In this talk, we will explore several functional programming concepts and techniques, lifted right out of high school algebra, that can deepen your functional programming skills and get you slicing your problems along new dimensions.
Video
Slides
Transcript
So I have a daughter. She's five. And a couple years ago, when she was about three. She was learning to count and she already knew how to do like 1 2 3. She could count out loud but I mean she was learning to count objects which is a little more complicated.
One of the cool things about having a daughter or a kid is that, they are beginners at everything and I love watching beginners learn something that I already know. Like I'm pretty good at counting. I make it look easy but it's not easy.
And just by watching my daughter, I could see how many ways there were to fail. That it was a real process that you had to get right. And I like going down into these basics and these fundamentals. And really uncovering something that to me is I've done it so long. It's so intuitive I don't have access to it anymore. But when I watch her I have access again. And I can say, oh! I see what I do when I count because of the way she messes up. Basically.

[ So let's go over this process of counting. So let's say we have some rocks. And I line them up so it's easier to count. And so here's the process. You get into a rhythm and you say 1 2 3.]
[Ok. At the same time, each time you say a word, you touch a rock. So you go 1 2 3 4 5 6. And then when you've touched all the rocks, the last number you say and the last word you say is the count of the rocks. As long as you do it right, you don't skip any and you don't do any twice.]
[So that's cool. We have a process for turning some real-world thing. A collection of objects into data, into a number. And then, we can use that number in other ways. And I feel like this is really fundamental to what we do as programmers. That we're always dealilng with processes and often we generate data off of that process and just to go deeper into this mystery.]
[Let's see. lf we projected out ten years and she starts collecting tons of rocks, a lot of rocks every day more than she does. Now because the trend continued, she's at the end of her day. She empties our pockets. Her bags she puts them on a table and she counts them. And then every day, she just records some information about the day. The date you know the weather and how many rocks she collected. And then at the end of the year, she can do all sorts of cool stuff with this data. She can sum up how many rocks did I collect this year.]

[What was the average number of rocks per day? What was my biggest week? What was my smallest month? She can do all of this stuff. For instance, the number of rocks in the year. She can do that without ever touching the rocks again. And we trust. All of us in this room trust that if she counted them each day correctly, and wrote them down correctly, when she adds them all up. She would get exactly the same answer as if she took those rocks that she put in the closet for the year and counted them out with that same process she started with.]
[And to me, that's like very mysterious. She's not touching rocks anymore but she's talking about, she's discovering ][stuff about the rocks. she somehow modeled some important aspects of the rocks with this data that she's collecting. and so that's something we do as programmers is we take some real-world process. and we turn it into some other process that a computer runs instructions in a machine. and these processes somehow get the same result. the same answer.]
[Somehow they're totally different processes. One is bits in a machine. It's moving stuff around in memory and the other is manipulating physical objects. So when we translate one process to another, there must be something that is preserved. Something essential to that process that goes from the physical process to the software process. So what is it that makes numbers as an example so useful for counting piles of rocks? That's the question I'm trying to answer.]
[So the title of my talk is All I needed for FP I learned in High School Algebra. It's kind of a fib because like I've already shown a lot of the stuff with to an FP. We started learning as soon as we were born right? We were playing with little things as babies.We developed these intuitive understandings of number and stuff like that.]
[Except in high school. We started going symbolic right? With an algebra class that's when arithmetic was no longer just some markings for problems we had to do in arithmetic right? This adding numbers it became talking about the properties of these operators that we had.]
[My name is Eric Normand. I teach Clojure online video form. Mostly at PurelyFunctional.tv. I also have a newsletter. A weekly newsletter. It's free sign up. I talk about Clojure and Functional Programming. It's a mix of news and history and other cool stuff I found around on the internet. And I'm also running a conference in New Orleans called Clojure Sync. It's in February.]

[You all know strange loop. If strange loop is about the confluence of industry and academia. Clojure Sync is about software and its place in the history of humanity. And I feel like the Clojure community through the lens of Clojure because the Clojure community is I think a really cool community.]
[To talk about this stuff in right, we were obviously philosophical programmers. Okay so like I said, I like going basic. Please don't think I'm talking down to you or like I don't think you know how to count or something like that I love doing this. I do it myself with my daughter's rocks with her. You know. I do it myself not by myself.]

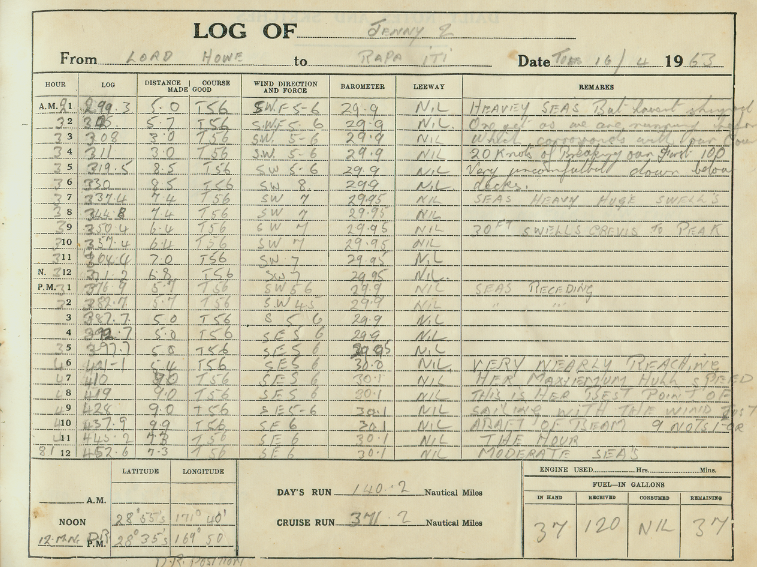
[Okay so let's imagine we had a pile of rocks. We'll call it A and we add to that another pile of rocks and that's B. We get this bigger pile of rocks. We can call that A plus B. Now we could also go he other way. We could start with the small one B and add the bigger one on top and pile of rocks at the end. At least the structure is different. Like the pile is different. Like the arrangement of rocks but the count is the same right? And we learned this as kids and there's something about this where the four combining rocks order doesn't matter.]

[We need to preserve this when we translate it into our information system into our log book. We need to preserve this order. Doesn't matter because we want to be able to you know, we can add up from the bottom. We can add up from the top. It's all the same right? We know that.]
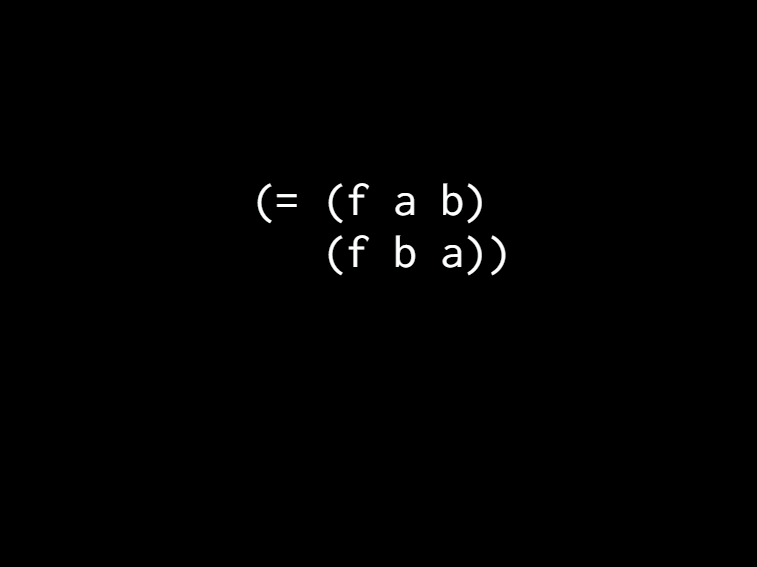
[So let's move into the symbolic realm. There's some Clojure code. We can also write this and we want to say that these are the same. So we can put in equals. So we've just derived this property of addition that the order of the arguments doesn't matter. And then we can pull this algebra trick and say we can actually say this about any function that we want to write. We could say, hey it has this property! Our order of arguments doesn't matter and mathematicians have called this commutativity.]
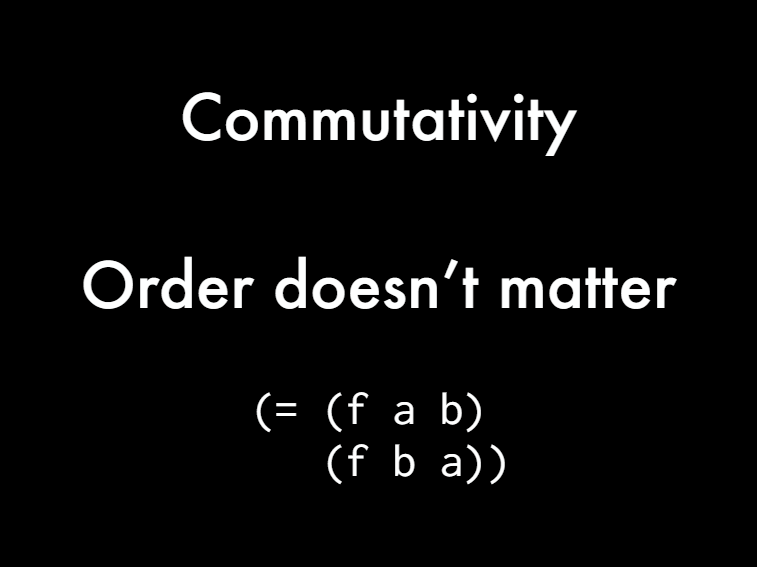
[Order doesn't matter. And the reason I'm bringing this up is commutativity is a great property. Mathematicians been talking about it for a long time. But we just derived it really quickly and we can derive all sorts of properties that we want. This is just one that Mathematicians happens have already discovered. But in your domain, the one you're modeling in your software, you have to go in and like figure out what are the things that are important to keep another thing.]

[What's cool about this is starting from the formula or the Equality that we have. We can make a test check property really easily. So of course, the generator has to be right. But if we got that all right, we've got a test check property that we can now guarantee that our function f is commutative using test check.]
[Okay. And now, I was gonna save this to the end but Rich talked about this in the morning so I have to mention it. So I am not trying to say that math is like the perfect thing and we should all be programming more math. And what I'm trying to say is that, Math is this platonic world where everything is consistent. That's like how you derive more math. You just stay consistent. You can do whatever you want.]
[But in the real world, we and we're modeling real word processes. This is much more messy. We don't have this strict line between what is commutative and what isn't. Sometimes the line is blurry. Sometimes there's conditions on it. Here's an example if we have merge of two HashMaps.]

[I could say and I'd be wrong but I could say it's commutative. It's not commutative because what if you have key collisions between the two maps? One of them is gonna have to win right? But when I'm programming in Clojure. And this is true in most dynamic languages.]
[I know at this point in my program, A actually is a map from over here and B is a map from over here. I know the keys and they don't collide right? That's how we program. We keep this stuff in our heads as we're programming.]

[ So if I just change the generators and I say well if I gen if A is a map 1 and B is a map 2. I can now say that because they have different keys that it's commutative.]
[So I'm just like elaborating this kind of absolute property called commutativity. Commutativity and tweaking it a little just for my purposes because that's how my model works. So we're taking the idea from math. Making it much more real world applicable.]

[ Alright. Now I said before that at the end of the year, my daughter would like to add up all the weeks right? ][she would figure out how much? how many rocks she had per week? how many rocks she had per month? and that's cool! she can group them by week. she can group him by month. she can group him by the whole year. she can say well how about each day was monday. bigger in general than tuesday then wednesday. she can group them arbitrarily. that is the cool property that comes straight out of piles of rocks. that's something that got preserved so let's take a look at that.]

[So we have these piles of rocks. We have two choices. We can group the ones on the left first. And then add in the other one.]

[Or we can start with the ones on the right and add in the third one. There's also the third choice which is just put them all together at once. Which is what we do in Clojure right? To have a plus with a bunch of numbers because we don't like to write extra parentheses in Lisp.]
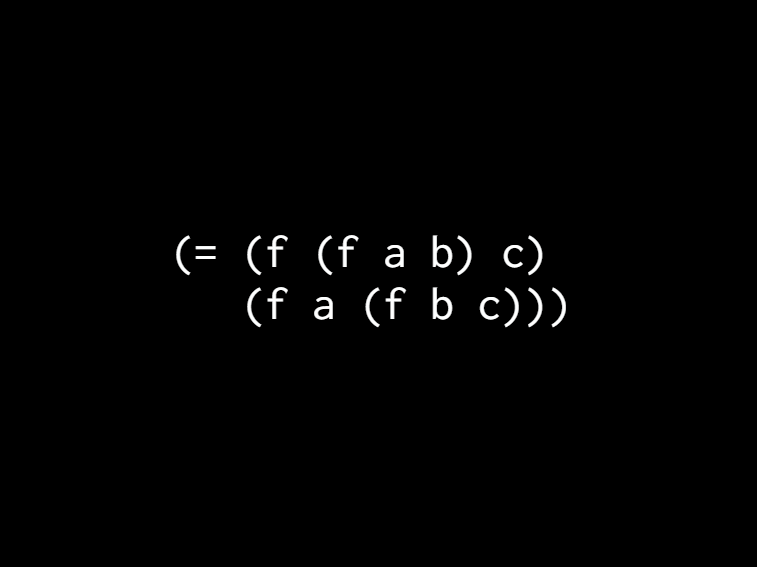
[What this means is grouping doesn't matter. ][i can group by month. i can group by week. grouping doesn't matter just to derive this. i can group there by the first one or the left ones are the right ones. and then i can put the other ones around it. and then i can get rid of the white space. and then i can say they're equal. so we just derived this little property that we can now use from test checker. you know just keep it in our head. make a comment. something like that. and then we can say for any function not just for addition.]
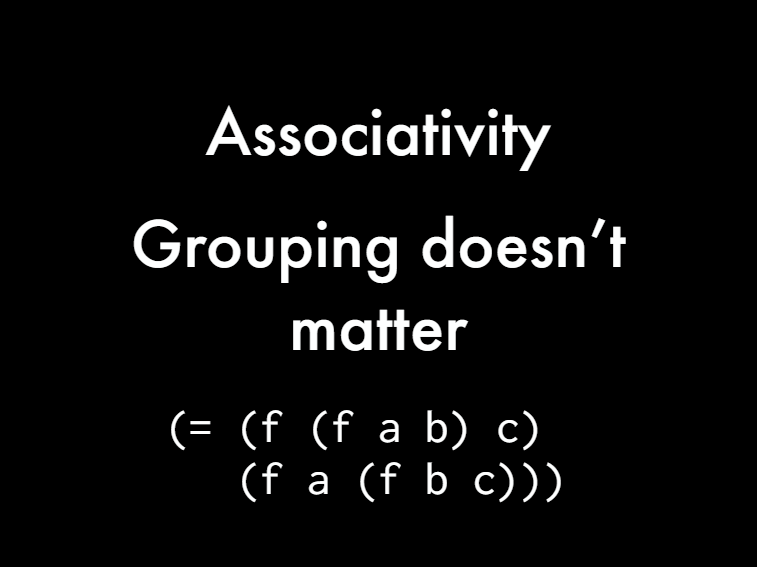
[This is called the Associativity and it's another one of those properties that algebra is talked about means grouping doesn't matter.]

[Okay. Let's go deeper into this one because the Associativity is actually a really cool property. That's not evident from what I've talked about. Like how cool it is? So I'm talking about types but I'm not beings. I'm dynamic typing right?]
[We're Clojure people but dynamic typing just like valid values for the arguments. So we see if we look at the first argument we've got. The return value of F is the first argument to F and A is the first argument to F. Which means that they have to be the same type. Same here. C is the second argument and F. The return value of F is also the second argument. So what we're saying is the return value of F and the two arguments to F have to be the same type.]

[Now I like to think of this as whole values. This is an idea from John Hughes. And this is how I think about it. If we have two piles, we combine them into a new pile. So it has all the same operations. The same properties as the individual piles had. Or if we have two strings and we are two lists and we concatenate them, we have a new list right? We haven't changed types. Same with merging two HashMaps. Where should HashMaps have a new HashMap? We're maintaining the space wherein we're still using the same type.]

[Okay. These two often get confused in high school Algebra. I got confused. I still use the words interchangeably. And wrong. I think it's because my teacher. And also just now, me we both used addition as the example which is both associative and commutative. So it's easy to mix them up but it's clear to see that the formulas are very different. ][and one's about order and one's about grouping.]
[Now, I've talked about some associative operations that aren't commutative like string concatenation or list concatenation. You can't reverse the order of the strings and get the same answer. But you can group them differently. I can do the ones on the right and then the one on the front. Or the ones on the left and the one on that right. Okay. But it's very hard to find a basic mathematical operation that is commutative but not associative. But you can make one. ][you just compose stuff up.]
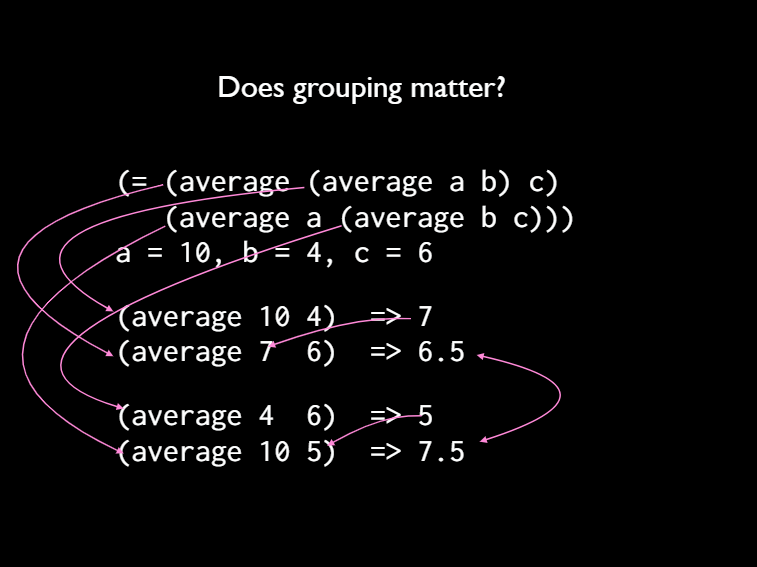
[ And so here's an example average so we can see if we're averaging two numbers. It doesn't matter what order we put A and B in right? But it's not associative. So let's look at the order. It doesn't matter. Just as an example. If we average 10 and 4 we get 7. If we average 4 and 7 or 4 and 10, we get 7. Same answer. But if we do grouping, so we add a third number C. It's gonna get tangled up with arrows here. But so we have A and B, 10 and 4 we get 7.]
[And then we average in that with 6. We get 6.5 or we could go on the second line. We can do 4 & 6 we get 5 and we average 10 with that and we get 7.5. So these are different. So it's the order. I mean the grouping does matter. The order doesn't matter but I want grouping to not matter. So we saw before how we could take a property that we discovered in the world and turn and and translate it and make sure it's preserved into our software.]
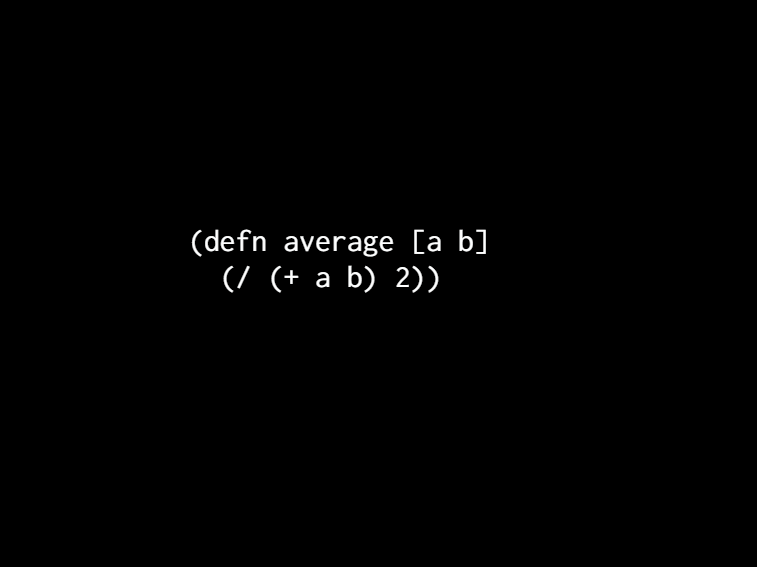
[But we can do this other thing where we take a software that doesn't actually have the property that we want and add it in. We can just do it. You just put it in there so we want it to be able to be associative. So let's do that. Okay. I often like to look at imperative code because the answers are often in there because if it works, it must have the properties that we're looking at. It's just that the properties are like smeared all over the boilerplate.]
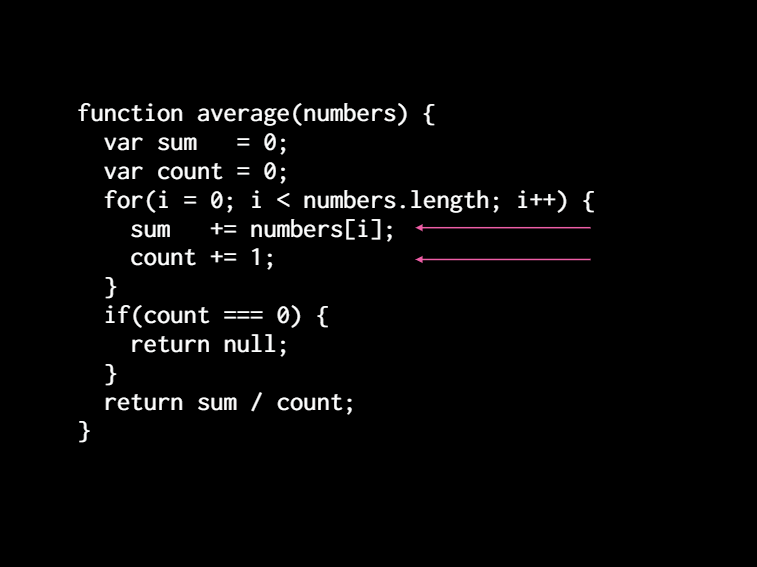
[So here we have a function average where you have an array of numbers. And you have ][to initialize some variables. and then we loop through the numbers and we accumulate the values into our variables. then at the end, we divide and we have this kind of case where if it's 0. we don't know what to return. so here returning mill that doesn't matter right?]
[Now I want to show this part. This is what we should focus on, is that at each iteration through the loop, we have a complete number and count for the things we've already seen right? We and we're grouping them like from the left of the array one at a time. Because we're associative, we can do that. We can group that addition any way we want. But the thing is, we've separated them. We don't have that whole value property. We have a sum and one number and a count in another so let's put them back together.]
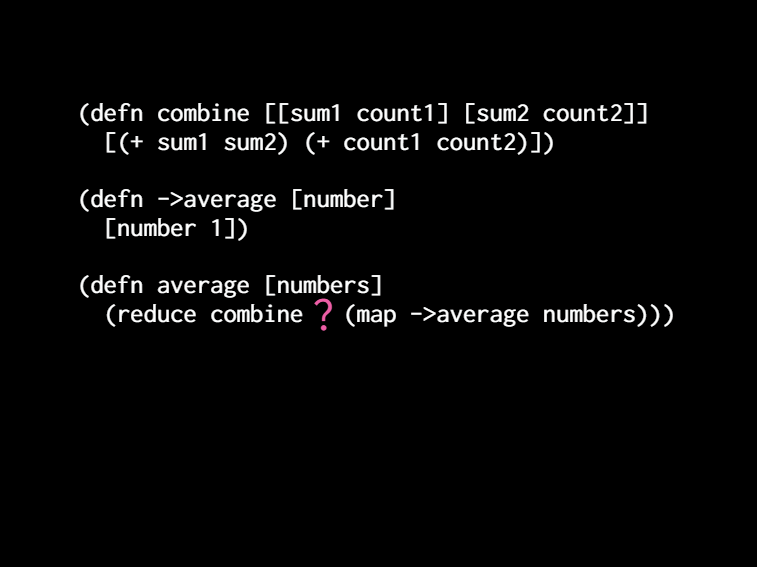
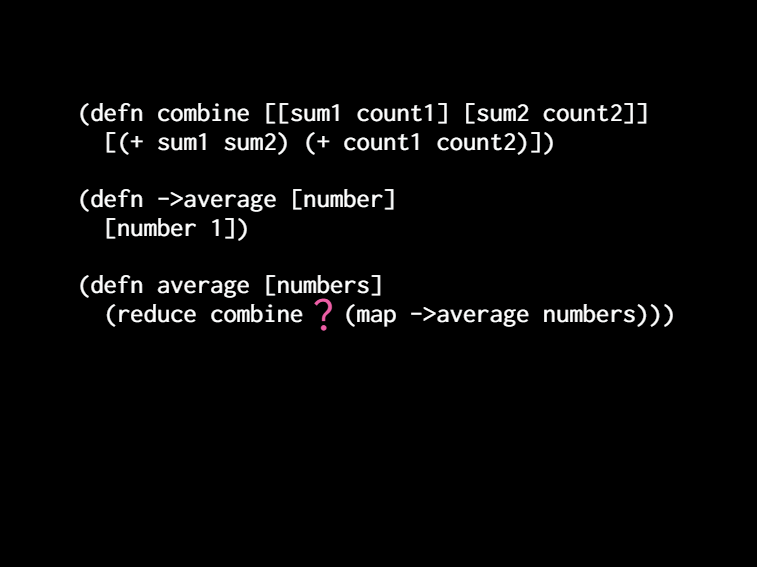
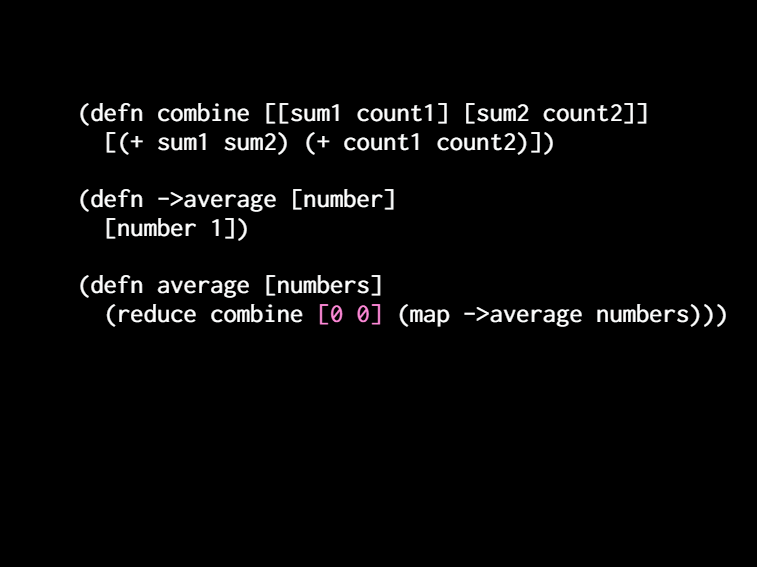
[Let's define a function called combined. And it's got it too. It's we wanted to be associative. So it's got to take two arguments. And so we'll take those sum and count and we'll tuple them up. So I'm gonna call that tuple of a summon account an average. It's a ratio. It's the numerator and the denominator of the average. We just haven't divided ][them yet. we're just keeping them separated. and so we also know that the return value has to be that same type. ][How do we get it? Well, we know we're adding up before we were grouping from the left. Now we're grouping arbitrarily.]
[So we're just gonna sum up the sums and sum up the counts. Okay. Now we can create a function called 2 average which is going to take a number and turn it into an average and so a single number. The average you know the denominator would be 1. So we just derived that tuple of number and it's in n1. And then we can write a function called average which takes that list of numbers and it maps to average over them. And then it can just reduce combined on them.]
[Okay. Now we have a problem. That we what we do in the if numbers is empty. It's an empty list. I don't recommend using the two argument version of reduce. We need an initial value there. So we're asking the question: where we start? Where do you start a computation? What do you like? If I tell you here's some rocks put them into a pile. Where do you start? You start with like a space on the floor and you call it an empty pile. And then you start adding the rocks to it right? Or if I say here's some rocks, count them. Where do you start? We're programmers so we start at zero. That's what you would initialize. ][you think to and then you just add 1 at 1 at 1. ]

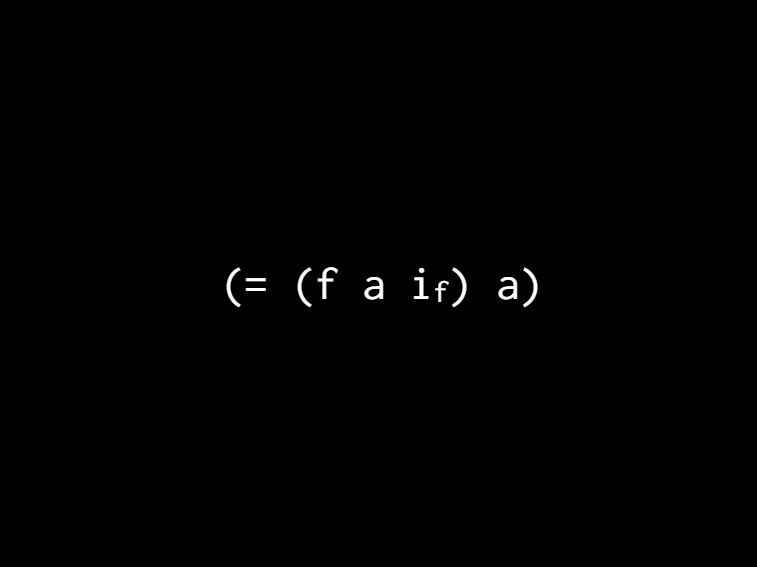
[So we have this thing in addition where we know we're starting at zero. So we know that adding zero to A will give us A and in general, we can do the algebra trick. Swap out the plus for any variable and we can say that F of A and which corresponds to the F. So I put a subscript even though that's not Clojure. But that I corresponds to the function itself right? Like each function might have a different value of I and so we can call this an identity value.]

[So in addition, the event of an identity value of zero in this concatenation it's the empty list etc. It just says where to start as a very simple formula.]
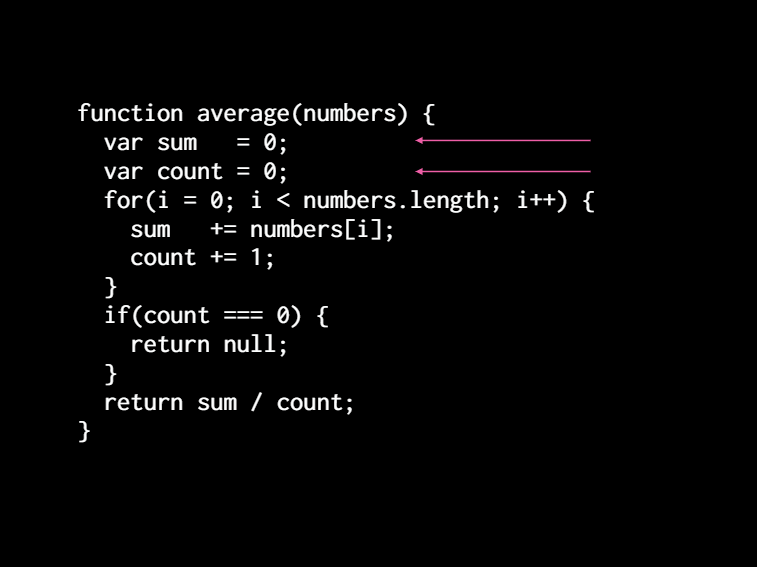
[And now we know what to put there. We go back to our JavaScript code and we see. ]
[Hey! That's what we initialized our values too. That's where we started at zero zero and so we'll just put that in there. Now we're not dividing them. ][so this is okay. it is a ratio of zero and zero. but we have not actually divided them. but what we have now---which we didn't have before was an answer to the question of what is an empty average?]
[An average of zero numbers we have. A value that we can check is this. The empty value because before we had null. Which doesn't really work with numbers. You're like, you're probably gonna do some other math with. No you're gonna get a null pointer exception. So you haven't really solved the problem if you've returned zero which I've done before to you. Confound it with the actual average zero so you don't know if you have nothing or we have something now.]

[Alright. Monoid. Monoid is where it's at. I don't know why everyone's talking about monads all the time but Monoid are where it's at and we just made one. It's any operation that has its associative and has an identity value. That's all Monoid it is. And they're way more useful. Way more common than ma monads and they're awesome for functional programming. And we should be talking about mono. It's one. Maybe we don't need to use the name but you know, there it's.]

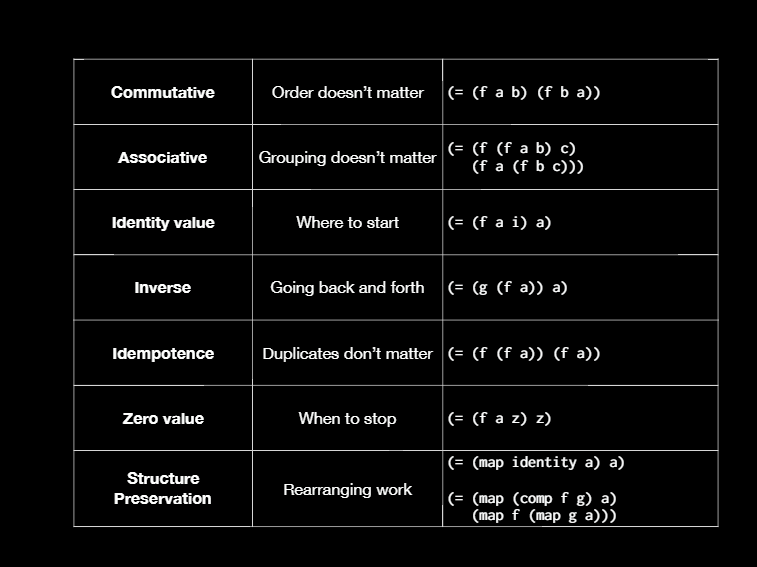
[Okay. Here's the table with everything we learned so far. Alright. Here's another property that is so basic like it's even silly to talk about. But like let's say I'm hungry and I don't want to cook, I go into a restaurant. I get my food. I eat it and then I leave right? I'm glad I can leave. I don't want to live there. I just want to eat. I didn't want to read a book so I go to the library. I read the book and I leave. I don't want to live in the library. I want to come back out. I want to go up the top of the mountain come back down. I want to get dressed and get undressed.]

[There's operations in the world that we want to preserve. That we can go back and forth on because going back and forth matters. We want to be able to move into a space where the sum calculation is possible or way easier. And then come back out because that's not where we want the answer. We don't want the answer in that space. When I say space, I mean like type right. So going back and forth matters.]
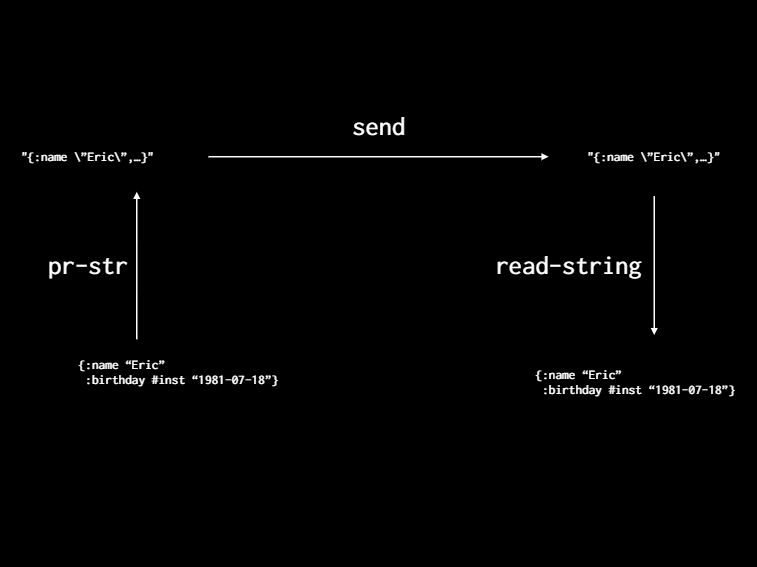
[Here's an example. Rich actually talked about this. I think he saw my slides which is why his talk was so good. Okay. So we have some value at the bottom left. Some map with my name and birthday. We need to send it to another computer to do some work. So we print it to a string and now that it's a string we can see. We can send it over the wire. I couldn't do that. It's just a regular data structure and then he can't he doesn't want a string. He wants a data structure on the other side so they read it in. And now it's a data structure you can operate on and do other stuff. And then you can do the reverse for the answer right? ][that's awesome it's awesome that we can do this. ]

[And so just symbolically, we can kind of derive this. So we have print string A and then we read that. That should be equal to A right? This is a really cool property. And we can do the algebra trick and say F of A and G of that it's equal to A and in that case, we say G is the inverse of F. And what it means is going ][back and forth matters.]
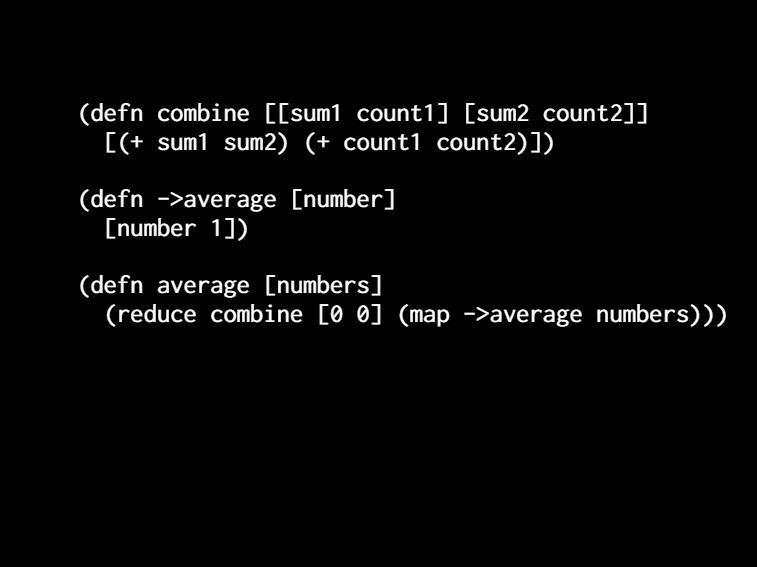
[So this is another property that you can derive from your code. You can turn into tests check properties. You can add it to your software. And now we can add it to this. So we already have a way of taking a number and moving it into this space where it's an average.]

[ It's a ratio we need to be able to come back down so we can write a function called average too. Which takes that tuple, the sum in the count and divides them right? And then our average function just becomes this. Really clear step-by-step thing. Take some numbers, lift them all up into the average space. Reduce with combined and then lower it back down. And this is a very common functional programming pattern.]

[Ok. Elevator buttons. Who knows what property I'm going to talk about? Now so you walk into an elevator area. You press the button and then someone else comes in. Button still lit up. They come and press it. Did they need to do that? No. But we have the habit or we have the like irresistible urge to press that button even though it's already pressed. But it doesn't matter that that second press did not matter.]

[In general, we could say duplicates don't matter for some operations. So here's another operation where duplicates don't matter and start with a HashMap em we Assoc a and hello and then we do it again. We know that. That's the same oops!]
[That's the same as doing it once and it even looks funny. Like why would you even think of writing this and doing this. Well I think you're seeing it backwards if you're asking that because it's more like I want to be able to do that and not worry about it. I don't have to care. I can do it as many times as I want and it's the same as doing it once. So we can ][do the algebra trick again.]
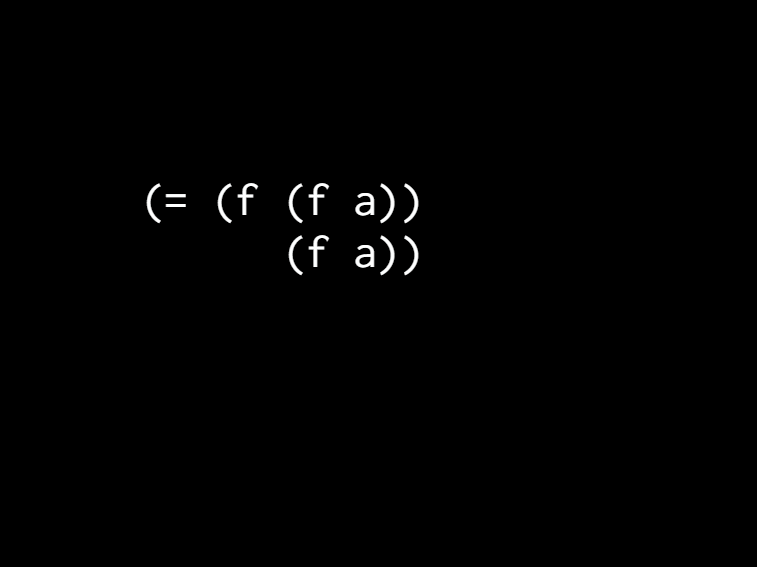
[We can say we know F of A is equal to F of A. But then, we can go boom do it again. Still equal. This is called Idempotence. Probably guessed that because we talked about that it's programmers. It's like the one algebraic property we're not afraid to name and it just means duplicates don't matter. ]

[Okay. So let's say we want to implement this. You want to implement an elevator button system for like the whole hotel. And we want to maintain this item potent property. So all we have to do is use an operation that already has idempotence and we're done. So a so John a HashMap has that. So we put in an Adam cause it's mutable. And then we can define a function called press.]

[Now here's the thing. It takes a button ID when you're using Idempotence often. You have an identity. The value has some kind of identity if you're adding to a set. So you add this the number four to a set twice. The second time doesn't matter right? What is the identity it's itself alright for its identity. But when you're adding to a HashMap, what is the identity? It's the key right? The key is the identity so we're gonna use that button ID as the key to a social. Just put through. It doesn't really matter what we put in there and we do some code later on. We get a press and we identify the button by its location and the direction. It's pointing to the third floor Northside UP button and you could press it multiple times. And we have this intuitive note a notion that the second and third time doesn't matter because we're gonna give the same state.]
[So we're done with Idempotence. There's more properties that I would love to talk about but every time I ran through this, it got complicated to explain and I ran out of time and I didn't get to conclude and talk about the good stuff. But just quickly a zero value when you're multiplying if you get a zero you can stop because you know the answer already. You have a zero so that's a zero value.]
[It tells you when to stop. And then structure preservation is this cool thing if you're in a factory and you have someone doing two operations on. An object it's assembly line right? As a manager, you can go in and say hey wait a second! Let's see if it's more efficient to split that two tasks into two people doing it one after the other. So it's the same assembly line but now you've split that one task over. But we know we'll get the same product out at the end. That's structure preservation. And so there's the formula for that right there.]
[Okay. Here's the conclusions translating these properties is what allows us to program. To translate from a physical to a software or symbolic system. And not only do we want to preserve these things and they're not these specifically. These ][were just examples right? it talked about that you can derive your own. you can add these to get those properties just like we did with the average example. and you can discover your own properties.]

[The trick is to make sure that they're simple and easy to test like we had. And you can tweak the ones that are well-known that you find in the algebra books. Because in the real world, there are these like corner cases and stuff that you have to deal with. ]

[Alright. Here's another thing. Here are some challenges of distributed systems that you know we all face when we start spreading our work over multiple machines. Messages are delivered out of order. ][well, if we just had something where order doesn't matter, that's okay. ]
[Messages are delivered one or more times well if we just had something where duplicates didn't matter. Now that's okay. Sending tasks and combining answers well if we had everything we needed for the tasks to be done bundled together and the whole value. We could just send it. And then we know that however it gets grouped in the Hadoop cluster and like recombined. It's okay because we can combine it back together and get the same answer. Where do you start when you're starting some work? When you start at the identity value and then serialization deserialization. ][we need to be able to turn it into something that we can send and then turn it back into data we can use. ]

[Okay. I talked about this algebraic properties. Make great tests check properties. I think I already mentioned this right? So we can test as an example. The commutative property of multiplication really easily. It's just this. It's a great. I love test check and people always wonder. Like how do you figure out what properties to actually test? Well you just come up with this little identity. There's a little equality and there you are. You have something to test. Something from the the thing you're modeling.]
[Okay. That's it! It's my talk. Oh! I forgot something. One thing before you walk out. I wanted to thank Guy Steele because a lot of these ideas come straight from there. He's sitting in the back. Thank you.]